Bayesian Multilevel Uncertainty Quantification for Enhanced Reliability Assessment and Decision Support
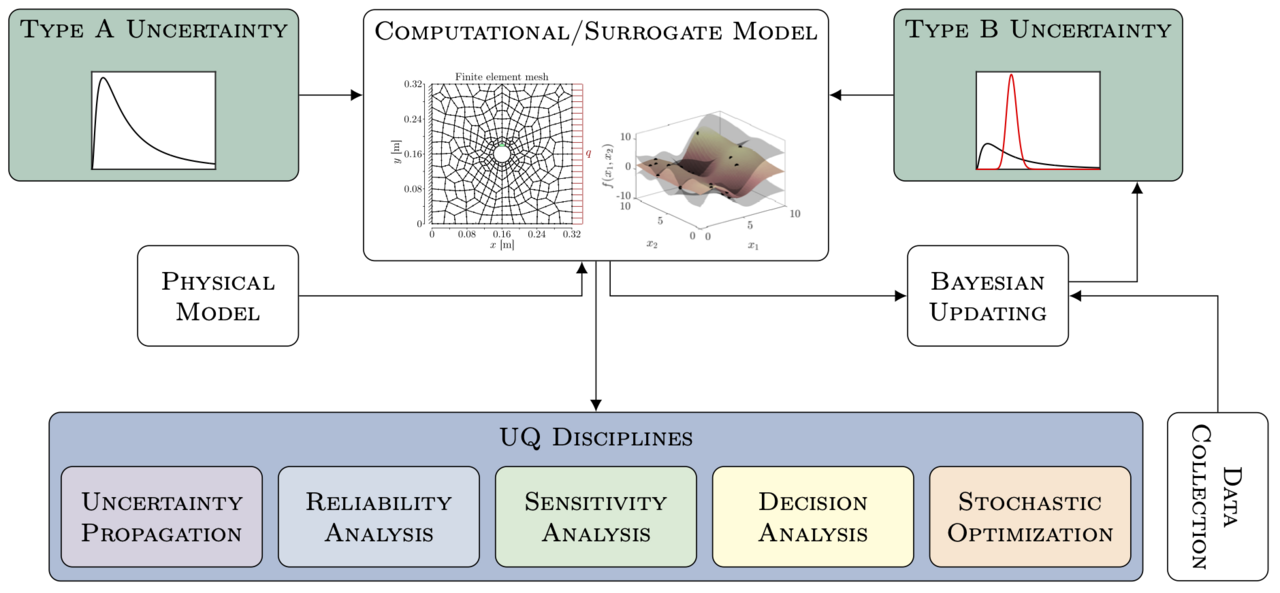
In a first phase of this project (see completed research projects: 'Uncertainty Quantification & Separation in Engineering Models'), we formulated a general framework for Bayesian multilevel uncertainty quantification (UQ), which is illustrated in Figure 1. The framework rests upon the separation of uncertainties in types A and B and the description of type B uncertainties with subjective probability in the Bayesian sense. Our goal was to express quantities of interest (QoI) such as the probability of failure (in reliability analysis) conditional on type B uncertainties. This establishes a functional relationship between the QoI and the type B inputs, which we examine, e.g., using variance-based sensitivity analysis. In the first project phase, we set out the framework and developed surrogate-assisted as well as surrogate-free sampling approaches to efficiently estimate such conditional quantities of interest.
Based on the outcomes of the first project phase, in particular the overall Bayesian multilevel UQ framework and the developed computational methods for its implementation, in this project phase we intend to further improve on the efficiency and accuracy of these approaches that are required for Bayesian multilevel UQ. In particular, we develop improved adaptive sampling methods for reliability assessment and Bayesian analysis. We use these efficient methods for computing required conditional QoIs in a decision-theoretic setting, where they enter the utility function.
Finally, the multilevel UQ framework has been initially used for enhanced reliability analysis, wherein the quantity of interest is the probability of failure. The latter is the expected value of an indicator function. For this reason, the methodologies and framework developed can be extended to cases in which the interest is in any other expected value, e.g., the variance of the model response. Applications of this generalization exist, e.g., in robust design optimization.
Researchers
Funding
DFG
Collaborations
Publications
- Max Ehre, Rafael Flock, Martin Fußeder, Iason Papaioannou, Daniel Straub (2022), Certified dimension reduction for Bayesian updating with the cross-entropy method, accepted for publication in SIAM/ASA Journal of Uncertainty Quantification.
- Max Ehre, Iason Papaioannou, Bruno Sudret, Daniel Straub (2022), Sequential active learning of low-dimensional model representations for reliability analysis, SIAM Journal on Scientific Computing 44, B558 - B584, https://doi.org/10.1137/21M1416758.
- Daniel Straub, Max Ehre, Iason Papaioannou (2022), Decision-theoretic reliability sensitivity, Reliability Engineering & System Safety 221, 108215,https://doi.org/10.1016/j.ress.2021.108215