Soil Dynamics and Soil-Structure-Interactions

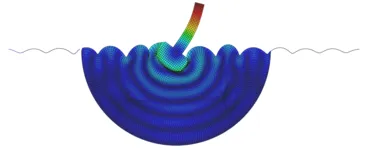
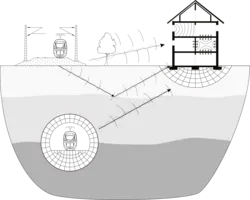
Several natural and human-induced processes can cause the propagation of waves in the soil, which can lead to the vibration of neighboring structures along with undesired or even dangerous effects.
For low level of the strain (approximately < 10-4), the soil vibrations can cause serviceability problems in the neighboring structures. Typical serviceability problems are train-induced vibrations and re-radiated sound. In cases such as seismic events or explosions, the level of vibrations and strains in soil and structures can increase significantly, leading to a safety problem. In both serviceability and safety case, it is important to es-
timate the response of the whole soil-structure system
accurately.
Depending on the level of the strains, the dynamic behavior of the soil-structure system can be considered linear or nonlinear and different simulation techniques exist for the two cases. At the Chair of Structural Mechanics different approaches are developed and used for solving different kind of linear and nonlinear soil-structure interaction problems: train-induced vibrations, vibration reduction measures for soil waves, seismic soil-structure interaction issues, etc....
Linear approach
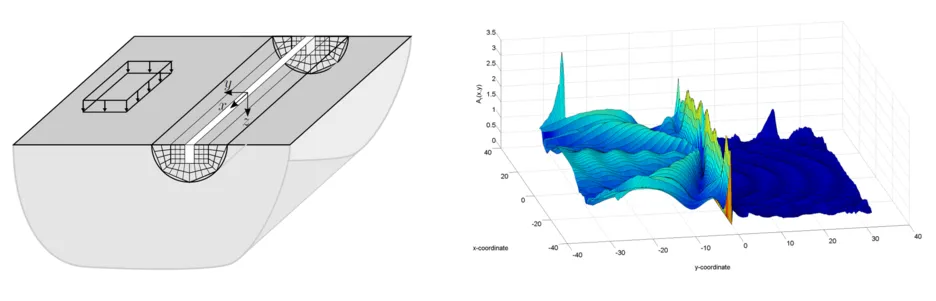
Harmonic or moving loads on the surface of the soil or inside a tunnel can lead to disruptive vibrations in structures located in the vicinity. Due to a growing sensibility of both, humans and machines, the importance of the prediction of oscillations due to rail or road traffic is increasing. Therefore, there is a need for a realistic model the total emission-transmission-immission system and thus the Soil-Sturcture-Interaction (SSI).
An appropriate description of the emission and immission systems, that usually exhibit detailed and complex geometries, can be achieved by the Finite Element Method (FEM). The limitations of this approach lie in the lacking possibility to model semi-infinite or infinite systems. As the Finite-Element mesh is limited, artificial reflections from the boundaries of the mesh arise, which create errors compared to the real infinite system. The Integral Transform Method (ITM) provides an analytical solution for the wave propagation in infinite media and therefore enables the modelling of the infinite soil without spurious reflections at artificial boundaries. By coupling the two methods the advantages of both methods are combined to model the total system as accurate as possible.
Dynamic stiffness matrix of the far field
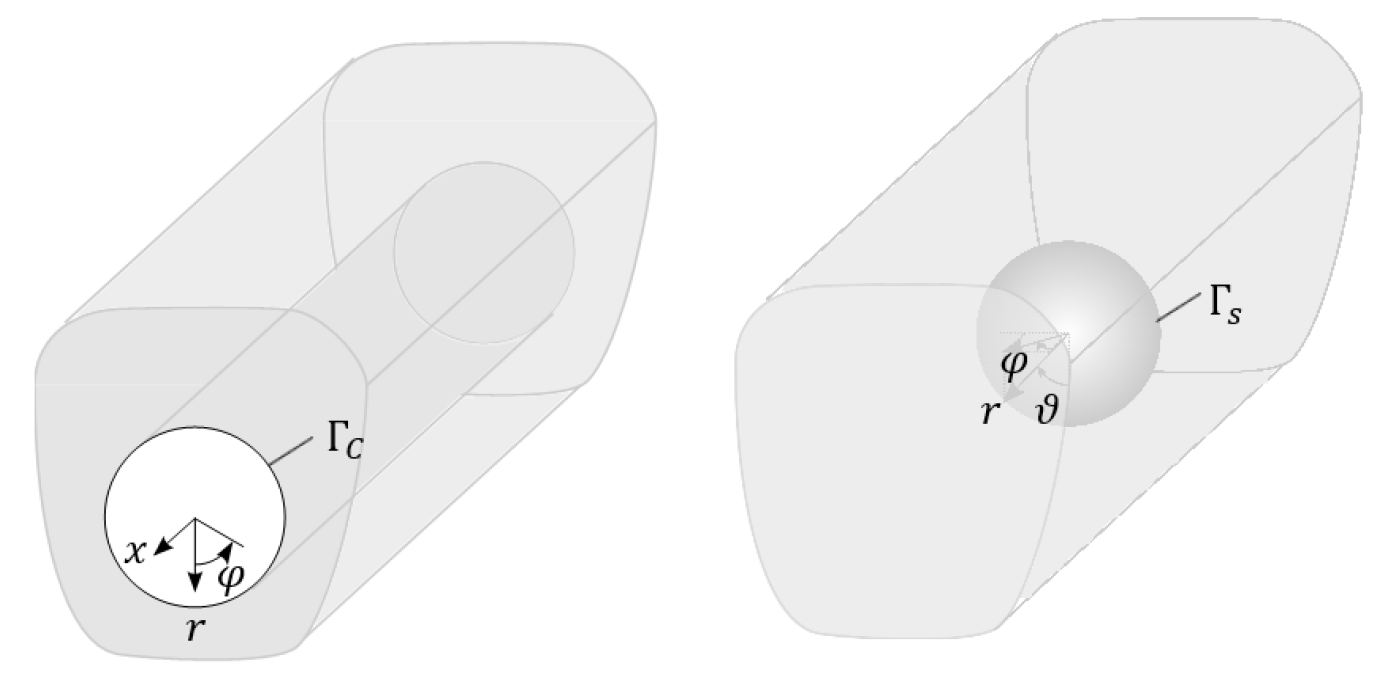
For a linear elastic continuum, the Lamé equation can be solved using the Helmholtz decomposition and a threefold Fourier Transformation. A system of three decoupled ordinary differential equations is obtained and solved with an exponential approach. Analogously fundamental solutions for a fullspace with cylindrical and spherical cavity can be deduced.
By the superposition of these fundamental systems it is possible to derive solutions also for further geometries like a halfspace with both, cylindrical or spherical cavity and cylindrical trench (2,5D) or a spherical indentation (3D). In addition, different soil layers can be included in the models. For the superposition, the stresses and displacements on the halfspace surface or the inclusion surfaces have to fulfill the real boundary conditions. Finally the equilibrium equations and thus the stiffness matrices are obtained.
Finite Element Substructure of the Near Field
To model complex structures and inhomogeneous soil conditions in the surrounding area the Finite-Element-Method is used. The stiffness matrices for structures with infinite extension in one dimension (2,5D) are calculated using a Fourier Transformed Finite-Element-Method formulation. For three dimensional structures common solid elements are used to compute the stiffness matrices of the FEM substructure.
Coupling of substructures
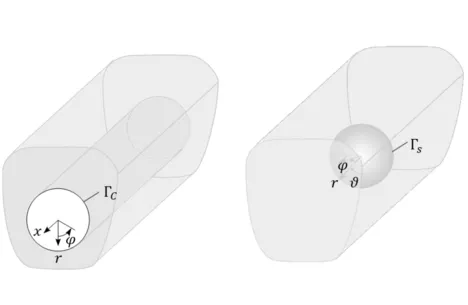
After calculating the stiffness matrices of the two substructures separately, they are coupled using the compatibility of the displacements and the equilibrium of forces on the coupling surface. As the FEM calculations are carried out in a 2,5D (for the cylindrical structure) respectively 3D (for the spherical structure) Cartesian coordinate system they are transformed into the associated coordinate systems of the ITM substructure (polar and spherical coordinate systems). Finally the stiffness matrices for the coupled ITM/FEM systems are obtained.
Examples of Applications
One possible application for the coupled ITM-FEM approach is the numerical prediction of the effectiveness of vibration reduction measures. The method facilitates to introduce mitigation measures at the source, the receiver or in the transmission path. Furthermore, the prediction of the environmental vibrations caused by machines or the reaction of structures due to an excitation in the soil is possible. Also moving load effects in the supersonic regime like the formation of a shock wave (Mach Cone) or the Doppler-Effect can be modeled with this approach.
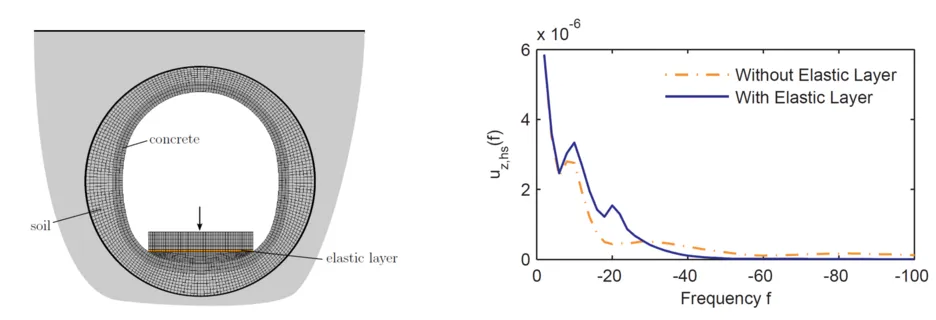
To reduce the train induced vibrations in tunnels an elastic layers can be inserted between track and tunnel thus creating a mass-spring system. The effectiveness of the mass-spring system can be predicted by a numerical model. The displacements on the surface of the halfspace are compared for the situation with and without elastic layer between track and tunnel.

Further reading
- Freisinger, J. and Müller, G. (2019). Modellierung eines halbraums mit sphärischem oder zylinderförmigem hohlraum für dreidimensionale boden-bauwerk-interaktion. Forschung im Ingenieurwesen, 83(1):31–42.
- Hackenberg, M. (2016). A Coupled Integral Transform Method - Finite Element Method Approach to Model the Soil-Structure-Interaction. Dissertation, Technische Universität München, München.
- Hackenberg, M., Dengler, M., and Müller, G. (2014). Implementation of the finite element method in the fourier-transformed domain and coupling with analytical solutions. In Cunha A., Caetano E., Ribeiro P., Müller G, editor, Eurodyn.
- Frühe, G. (2010). Überlagerung von Grundlösungen in der Elastodynamik zur Behandlung der dynamischen Tunnel-Boden-Bauwerk-Interaktion. Dissertation, Technische Universität München, München.
Contact
Nonlinear Approach
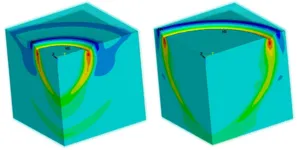
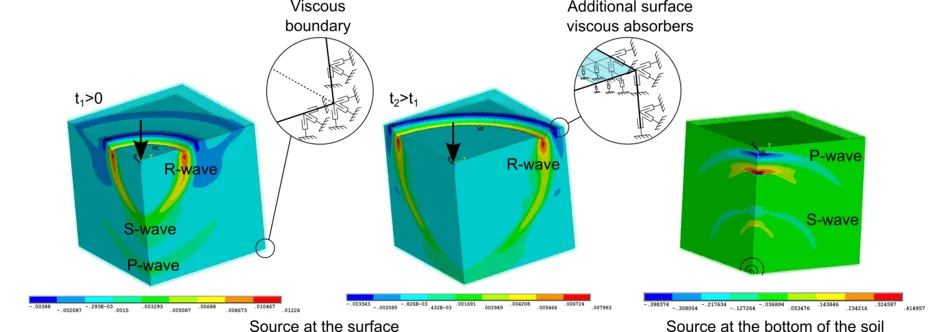
As for the linear case, the most common used model to capture the nonlinear behavior of the soil-structure system is a discretized numerical model using the Finite Element Method (FEM). Nonlinear analyses are usually carried out in the time domain (TD), using time integration techniques. Nonetheless, applying the FEM for the soil system cannot capture the real endless dimension and requires significant number of degree-of-freedoms (DOFs). Therefore, the FEM requires a special extension to account for the frequency-dependent properties of the soil. We develope and apply different direct and substructuring methods for nonlinear SSI. These range from simple 1D spectral methods to 3D transient approaches.
Lumped-parameter models
A lumped parameter model is a block of springs, dashpots and masses, able to reproduce the dynamic behavior of a soil-foundation system. Its real frequency-independent coefficients are found by approximating the dynamic impedance or compliance functions by a ratio of two polynomials. We developed extended LPM for horizontally layered soil and different form of the foundation.
Hybrid frequency-time domain (HFTD) methods
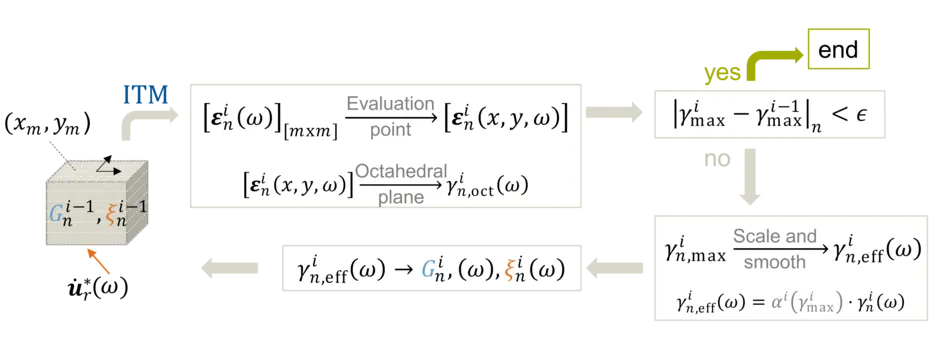
Hybrid frequency–time domain (HFTD) methods represent an efficient tool to study the strain- and frequency-dependent behaviour of the soil in a seismic SSI simulation. Most of the existing HFTD methods idealize the soil behavior according to the one-dimensional (1D) wave propagation theory, which is a major simplification of the complex three dimensional (3D) theory. We developed a HFTD method, where the soil is described as a 3D continuum governed by Lam´e’s equation of elastodynamics and the problem is solved with the integral transform method (ITM). The shear modulus and the damping of the soil are nonlinear functions of the strain level. The seismic waves (the loading) can be represented by spatial waves with an arbitrary distribution in time and space. The response of the soil to the seismic waves is first solved in the FD assuming a linearized elastic soil subjected to input waves, the response is transformed into the TD and the maximum strain is evaluated at different depths. According to the maximum strain, the shear modulus and the damping at different depths is updated and the process is iterated until convergence.
Coupling of the FEM with the SBFEM (in collaboration with the University of Braunschweig)
In collaboration with the University of Braunschweig, we proposed a strategy to investigate the vibrations of one or more buildings subjected to seismic loads, incldung the soil-structure interaction and the input spatial variability. The latter results from the propagation of seismic waves through the underlying soil and are governed by the Lam´e’s equations. The structure and its foundation as well as parts of the soil are modeled by Finite Element Method (FEM). The infinite half-space is discretized by Scaled Boundary Finite Element Method (SBFEM). Both methods are coupled at the common interface. The seismic excitation is expressed as a 3D seismic wave field and transformed into boundary tractions, which are then applied at the interface between the near and far fields. The proposed method can be used also to investigate the 3D nonlinear response of the near field, where nonlinear material properties can be assigned to any element of FEM part.
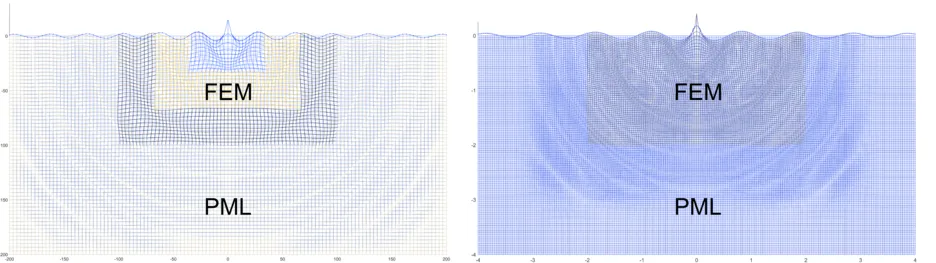
FEM with transmitting boundaries
Further reading
- Taddei F.; Nguyen T.H.; Müller G.: Hybrid Frequency-Time Domain Method for Three-Dimensional Seismic Analyses of Nonlinear Soils. 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 2019
- Taddei F.; Greim A.; Englert H.; Müller G.: Modelling the Seismic Soil-Structure Interaction for Wind Turbines Using Simple Physical Models. 2nd International Conference on Natural Hazards & Infrastructure, 2019
- Marco Schauer, Francesca Taddei, Sissy Morawietz: A Strategy to Conduct Numerical Simulation of Wind Turbine Considering the Soil-Structure-Interaction by Using a Coupled FEM-SBFEM Approach in Time Domain. IUTAM Symposium on Solver-Coupling and Co-Simulation 35, 2019
- Marco Schauer, Francesca Taddei, Gustavo Adolfo Rıos-Rodriguez: Seismic Transient Simulation of an Operating Wind Turbine Considering the Soil-Structure Interaction. Journal of Physics: Conference Series, 2019
- Taddei, F. ; Müller, G.; Lu, X.: Towards a nonlinear discrete model for site-city interaction through a Sino-European synergy. 16th European Conference on Earthquake Engineering (16ECEE), 2018
- Taddei, Francesca; Schauer, Marco; Meinerzhagen, Lisanne: A practical soil-structure interaction model for a wind turbine subjected to seismic loads and emergency shutdown. Procedia Engineering 199, 2017
- Taddei, F.; Butenweg, C.; Klinkel, S.: Parametric investigation of the soil–structure interaction effects on the dynamic behaviour of a shallow foundation supported wind turbine considering a layered soil. Wind Energy (18/3), 2014, 399-417
Contact
Francesca Taddei, PhD