Vibroacoustic simulations are used to assess the vibration behavior and sound radiation of structures. To capture the characteristic wave phenomena and the coupling between structure and acoustic fluid properly, a fine discretization of the numerical models has to be chosen. This results in very large systems of equations, which cannot be handled efficiently and are very computationally expensive to solve. Model order reduction (MOR) provides powerful tools to reduce the size of the numerical models while the system response of the reduced system does not change significantly. In the context of many-query analyses like optimization or uncertainty quantification, the vibroacoustic simulation has to be performed for different values of the input parameters. MOR methods that are capable of retaining the parametric dependency of the system in the reduced matrices, are called parametric Model Order Reduction (pMOR) methdos. These methods can be divided into intrusive and non-intrusive ones.
Intrusive Model Order Reduction
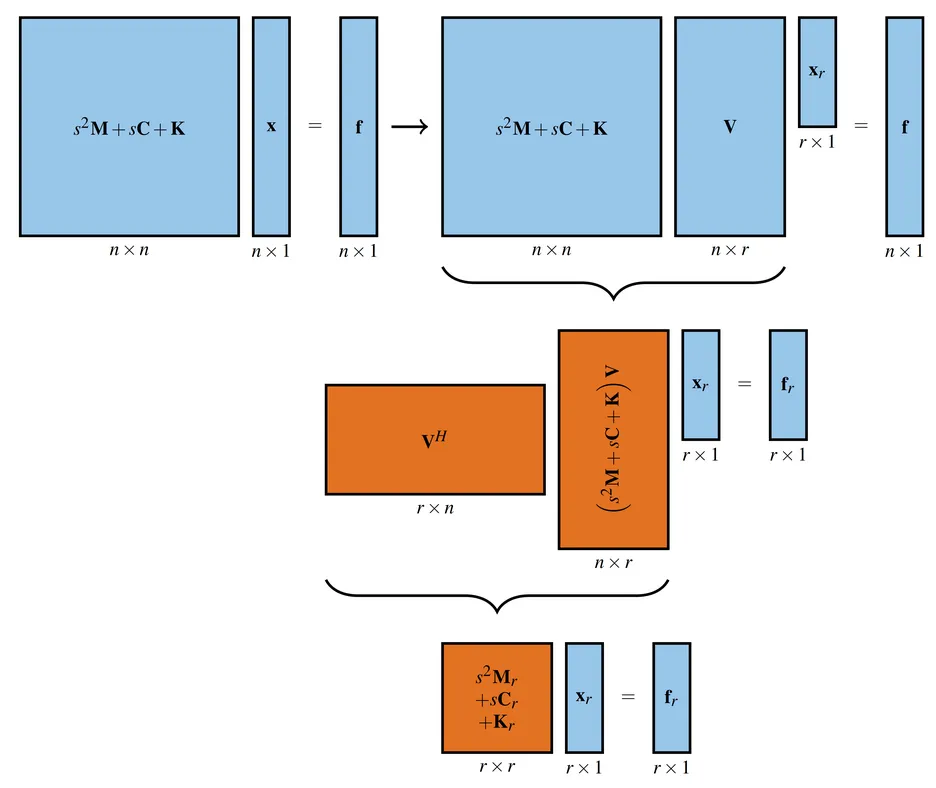
Intrusive MOR methods are often projection-based, which means that the full system is projected into a lower-dimensional subspace. If the reduced basis is chosen appropriately, the reduced systems yield very accurate results. Methods to obtain the reduced bases are for example modal reduction, which uses (eigen)modes of the structure for reduction or the Proper Orthogonal Decomposition (POD), in which the reduced basis is built from snapshots of the system's response at various frequencies. Parametric MOR can be achieved with these methods by different approaches. In the global approach, the reduced basis computed for different parameters are concatenated to one reduced basis valid for all possible parameter values. Local approaches instead interpolate either between the reduced bases or the reduced matrices for different sampled parameter values to obtain the reduced basis/matrices at an unqueried point.
Non-intrusive Model Order Reduction
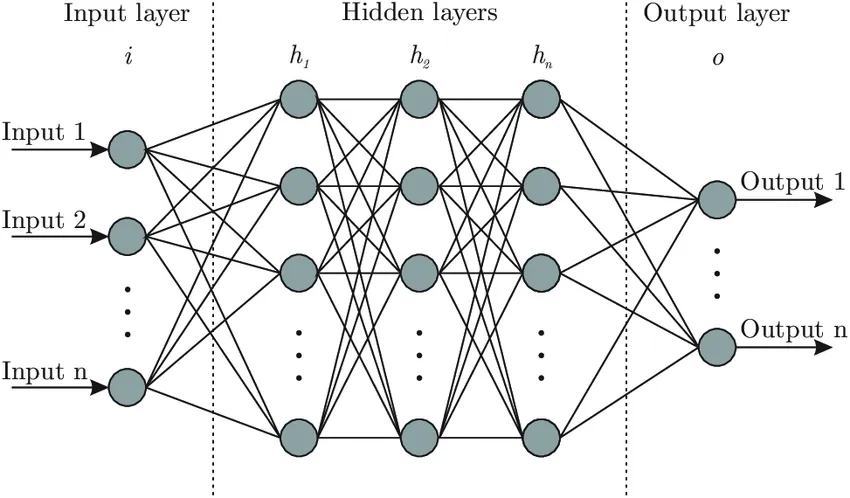
For intrusive methods, the full order system matrices (and thus the governing equations) have to be known and available to be able to perform the projection. In case this information is not available, non-intrusive MOR methods can be applied. These are usually data-driven methods, which means that they simply try to learn the relation between the input parameter values and the output (quantity of interest). These methods are often also referred to as Machine Learning methods. Since no information about the physics is included they are often less accurate than intrusive methods, but their range of application is more general.