Introduction
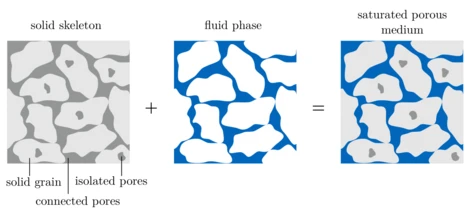
Vibrations in a soil medium can result from natural phenomena, e.g. an earthquake, or events related to human impact (see Fig. 1). Induced soil vibrations may affect nearby buildings by reducing the serviceability and can cause discomfort or health problems for residents. The soil material is often assumed to be an elastic continuum, even though it may consist of several phases, e.g. solid grains, water, air or oil (see Fig. 2). By applying an elastic model to a water saturated soil medium, one of the underlying assumptions is that fluid and solid phase stick together and share the same displacement field. For civil engineering applications, which usually deal with a frequency range from 1 Hz to 250 Hz, this assumption is sufficient if the soil medium consists, for example, of clay, gravel or cobbles. However, fluid and solid phases can vibrate differently in sands and fine silt, which needs to be covered by a poroelastic (numerical) model. Such a poroelastic model is provided, for example, by the Biot theory [Biot 1962].
The main challenge for a poroelastic numerical model is to deal efficiently with the additional degrees of freedom that result from the description of separate displacement fields for the fluid and solid phases. The Wave Based Method (WBM) presents an efficient numerical method to compute the steady-state solution for a boundary value problem. It is revealed for poroelastic materials in vibro-acoustic applications, that the WBM works significantly faster, more efficiently and with higher convergence rates than the Finite Element Method (FEM) [Deckers 2012]. These accomplishments motivated to extend the WBM for predicting ground-borne vibrations in poroelastic structures.
The Wave Based Method
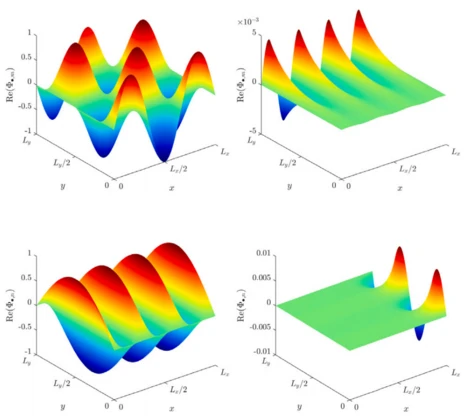
The WBM uses weighted wave functions to approximate the field response of a boundary value problem. In the case of a (poro)elastic medium, field responses encompass, for example, displacements, strains, and stresses. As shown in Fig. 3, each wave function consists of one part, either a cosine- or sine-function, which defines a standing wave in 𝑥- or 𝑦-direction. This is multiplied by a second part (e-function), which describes an evanescent or propagating wave pattern. The number of wave functions is truncated with respect to the highest physical wave number, which is approximated in the system.
The WBM was first initiated in [Desmet 1998] to analyze coupled vibro-acoustic problems in the mid-frequency range. The wave functions in a WBM model present exact solutions of the underlying differential equations of a boundary value problem. However, these wave functions do not necessarily fulfill the assumed or given boundary conditions. Therefore, the unknown weighting values for the wave functions are computed such that the sum of the weighted residuals for the applied boundary conditions is approximated. Due to this characteristic, the WBM is often named weighted residual Trefftz method or indirect Trefftz method.
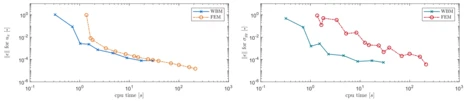
The WBM is mainly known for its high convergence rates (see Fig. 4) and for the fact that it usually needs significantly fewer degrees of freedom than a FEM approach. Modern approaches deal with expansions/modifications of the WBM to make it more flexible for geometrical complex structures, to use it for time dependent (non-harmonic) excitation, and to broaden its field of applications. In [Deckers et al 2014], an overview of the different enhancements in the development of the WBM is provided, which are primarily achieved at the Noise and Vibration Research Group of the KU Leuven.
Applications
Description of a 2D semi-infinite medium
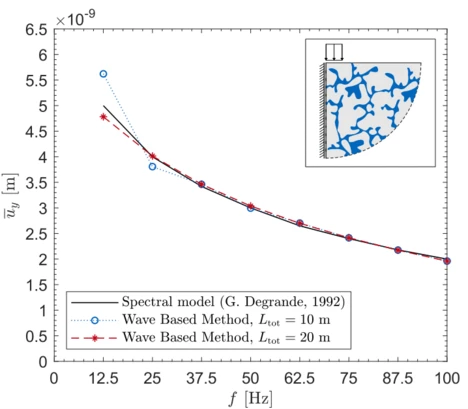
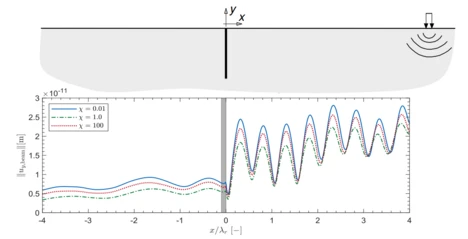
The WBM presents a domain based approach, subdividing a problem into several elements, whose field responses are approximated by wave functions. One big challenge for numerical methods based on space discretization is to mimic a semi-infinite soil medium with a bounded numerical model. Different concepts of absorbing boundaries are established to approximate the Sommerfeld radiation condition. This condition states that the energy in a system propagates to infinity and not from infinity to the system. To approximate the Sommerfeld radiation condition, the absorbing boundary condition (ABC) from [Degrande and De Roeck 1993] is chosen for the WBM, which is local in space and frequency dependent. The derivation of this ABC is based on the analytical solution for a porous medium, and permits perfect absorption of normal incident wave fronts. Fig. 5 shows an exemplary 2D poroelastic soil model with a surface loading. The mean vertical displacement amplitude is evaluated under the loaded strip by testing several excitation frequencies. The results illustrate that the WBM model with an ABC can adequately approximate the reference solution.
Modelling a wave barrier
The WBM can also be coupled to subsystems to model the interaction between a soil medium and a substructure. For example, such an approach is developed to couple a sheet wall to a poroelastic halfspace. The sheet wall is described here with an Euler-Bernoulli or Timoshenko beam model. Fig. 6 illustrates the normal and tangential stresses between a beam and two coupled WBM elements. These stresses depend on the wave functions from the left or right domain, inducing longitudinal and vertical displacements along the beam axis. To couple the beam to its adjoining WBM elements, element and coupling matrices are derived, which contribute to the final system of linear equations. Additionally, boundary conditions need to be formulated and added to the system of linear equations. Here, it is assumed that the sheet wall has free ends, so its internal forces are assumed to be zero at these points.
Sheet walls can reduce soil vibrations, which are induced by Rayleigh-waves. A train passage can cause such surface waves. Fig. 6 presents displacement amplitudes, which are computed along the surface of a soil medium with a sheet wall. The system is exposed to a surface load and tested for different degrees of coupling between the water phase and the solid grains. The highest displacement amplitudes are retrieved for strong coupling (blue graph) and loose coupling (red line). In the case of a medium degree of coupling (green line) between fluid and solid phase, viscous damping strongly affects the system, which reduces the computed displacements.
Wave scattering at a surface irregularity
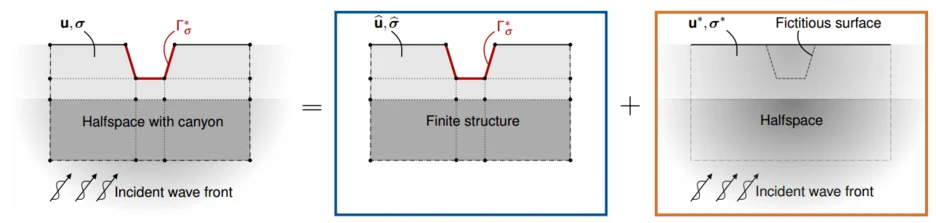
Ground-borne vibrations can also be induced by oblique incident wave fronts, often combined with reflection, refraction, and/or mode conversion processes. Incident wave fronts may result from earthquakes, underground trains, or energy generation processes (e.g. drilling platforms, geothermal power plants). Fig. 7 shows an example of a layered soil domain with an empty canyon, resulting, for example, from a dried river. The system is decomposed into a scattered wave field and a free field solution. The scattered wave field is modeled as a finite structure with the WBM. The free field solution is related to an incident wave front, which is reflected along the surface of the layered halfspace without a canyon. The direct stiffness formulation presented in [Degrande and De Roeck 1992] is applied to compute the free field solution. As shown in Fig. 7, the surface of the canyon is highlighted with red color, corresponding to a fictitious surface in the free field solution. The solutions for the scattered and free field are coupled along this boundary to fulfill the condition of an unloaded surface. For this, additional residual error functions are formulated and weakly enforced. After solving the system of linear equations, the total system's response is computed by superposing the solutions for the scattered wave field and the free field solution.
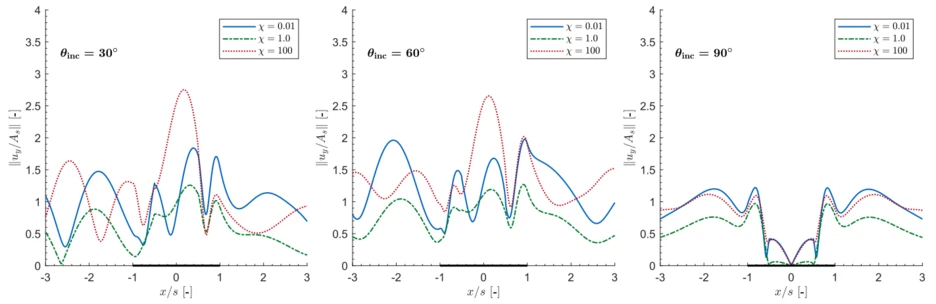
In Fig. 8, vertical displacement amplitudes are depicted, which are evaluated along the surface of a soil domain and canyon. These are computed for an incident S-wave. Different incident angles and degrees of coupling between the fluid and solid phases are tested. The highest displacement amplitudes are retrieved for strong coupling (blue graph) and loose coupling (red line). In the case of a medium degree of coupling (green line) between fluid and solid phase, viscous damping strongly affects the system, which reduces the computed displacements.
The numerical examples presented here are computed in the frequency domain and can be transformed into the time domain by applying an inverse Fourier transformation scheme. This permits the prediction of ground-borne vibrations caused by a time dependent signal (non-harmonic excitation), such as an earthquake. Fig. 9 presents an exemplary video for the vertical displacement field of a poroelastic layered soil with an empty canyon exposed to an incident S-wave. This wave front is described with a Ricker wavelet. The soil's water phase and solid grains are characterized by loose coupling. Due to this, the soil material is hardly affected by viscous damping. This state of loose coupling permits the visualization of a second P-wave (P2-wave), charactersitic for a poroelastic continuum described with the Biot theory. In Fig. 9, it can be seen that an incident S-wave arrives, which is refracted into a S- and P2-wave in the upper soil layer. These cause a scattered wave field around the empty canyon and generate surface waves, which propagate away from the canyon.
Further Reading
- Lainer, Mirjam: A Wave Based Method for the analysis of a poroelastic system with a harmonic or time dependent excitation. Dissertation, 2025, doi: 10.13140/RG.2.2.33805.86247.
- Lainer, Mirjam; Müller, Gerhard: A wave based approach for the assessment of fluid–solid coupling for a scattered wave field at an empty canyon. Soil Dynamics and Earthquake Engineering 200, 2026, 109827, doi: 10.1016/j.soildyn.2025.109827.
- Lainer, Mirjam; Müller, Gerhard: Efficient treatment of a thin-walled wave barrier in a (poro)elastic structure with the Wave Based Method. Computers and Geotechnics 186, 2025, 107409, doi: 10.1016/j.compgeo.2025.107409.
Lainer, M.; Taddei, F.; Müller, G.: A Wave Based Method for the analysis of a fully and partially saturated halfspace under harmonic loading. Computers & Structures, 2023, doi: 10.1016/j.compstruc.2023.107040.