Erschütterungen in wassergesättigten Böden
Einführung
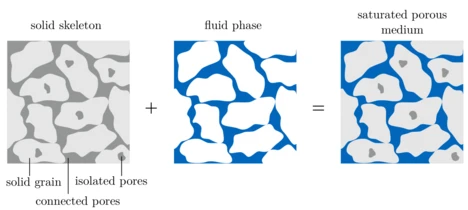
Erschütterrungen im Erdreich können etwa durch natürliche Phänomene, z. B. ein Erdbeben, oder durch Ereignisse im Zusammenhang mit menschlichen Einwirkungen entstehen (siehe Abb. 1). Induzierte Bodenschwingungen können nahegelegene Gebäude beeinträchtigen, indem sie z.B. deren Gebrauchstauglichkeit verringern. Zudem können solche Schwingungen den Wohnkomfort beeinträchtigen und gesundheitliche Schäden bei betroffenen Bewohnern hervorrufen. Das Bodenmaterial wird häufig als elastisches Kontinuum betrachtet, obgleich dieses aus mehreren Phasen bestehen kann, z. B. festen Körnern, Wasser, Luft oder Öl (siehe Abb. 2). Bei der Verwendung eines elastischen Modells für ein wassergesättigtes Bodenmaterial liegt die Annahme zugrunde, dass Flüssigkeits- und Feststoffphase zusammenhaften und dasselbe Verschiebungsfeld teilen. Für Anwendungen im Bauingenieurwesen, die üblicherweise einen Frequenzbereich von 1 Hz bis 250 Hz betreffen, ist diese Annahme ausreichend, sofern das Bodenmedium beispielsweise aus Ton, Kies oder Geröll besteht. In Sanden und feinem Schluff können sich jedoch Flüssigkeits- und Feststoffphasen unterschiedlich bewegen. Dieses Phänomen kann durch ein poroelastisches (numerisches) Modell abgedeckt werden. Ein solches poroelastisches Modell wird beispielsweise durch die Biot-Theorie bereitgestellt [Biot 1962].
Eine wesentliche Herausforderung für ein poroelastisches numerisches Modell besteht darin, mit den zusätzlich auftretenden Freiheitsgraden umzugehen, welche sich aus der Beschreibung separater Verschiebungsfelder für die Flüssigkeits- und Feststoffphase ergeben. Die Wave Based Method (WBM) stellt eine effiziente numerische Methode zur Berechnung des eingeschwungenen Zustands eines Randwertproblems dar. Für poroelastische Materialien in vibroakustischen Anwendungen zeigt sich, dass die WBM deutlich schneller, effizienter und mit höheren Konvergenzraten arbeitet als etwa die Finite-Elemente-Methode (FEM) [Deckers 2012]. Diese Ergebnisse geben Anlass zu dem folgenden Forschungsprojekt, welches sich mit einer Erweiterung der WBM befasst, um Erschütterungen in poroelastischen Bodenmodellen vorherzusagen.
Die Wave Based Method
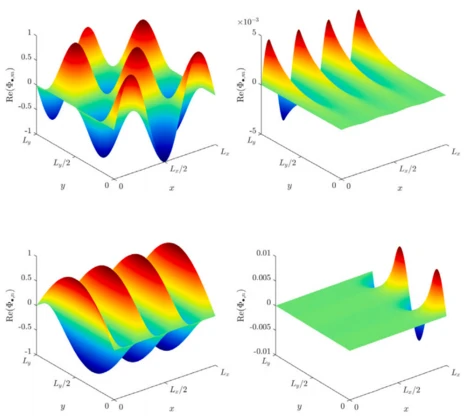
Die WBM verwendet gewichtete Wellenfunktionen, um die Verschiebungen, Dehnungen und Spannungen innerhalb eines Randwertproblems näherungsweise zu berechnen. Wie in Abb. 3 dargestellt, besteht jede Wellenfunktion aus einem Teil, entweder einer Kosinus- oder Sinusfunktion, die eine stehende Welle in x- oder y-Richtung definiert. Diese stehende Welle wird mit einem zweiten Teil (e-Funktion) multipliziert, der ein abklingendes oder propagierendes Wellenfeld beschreibt. Die Anzahl der Wellenfunktionen wird bezüglich der höchsten physikalischen Wellenzahl im System begrenzt.
Die WBM wurde erstmals in [Desmet 1998] beschrieben, um gekoppelte vibroakustische Probleme im mittleren Frequenzbereich zu analysieren. Die Wellenfunktionen in einem WBM-Modell stellen exakte Lösungen der zugrunde liegenden Differentialgleichungen eines Randwertproblems dar. Diese Wellenfunktionen erfüllen jedoch nicht unbedingt die angenommenen oder vorgegebenen Randbedingungen. Daher werden die unbekannten Wichtungen für die Wellenfunktionen so berechnet, dass die Summe der gewichteten Residuen für die zugrundeliegenden Randbedingungen näherungsweise erfüllt wird. Aufgrund dieser Eigenschaft wird die WBM häufig auch als gewichtete Residuen-Trefftz-Methode oder indirekte Trefftz-Methode bezeichnet.
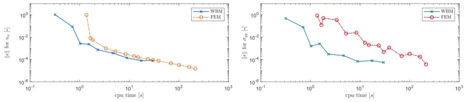
Die WBM ist vor allem für ihre hohen Konvergenzraten bekannt (siehe Abb. 4) und dafür, dass sie in der Regel deutlich weniger Freiheitsgrade benötigt als ein FEM-Ansatz. Moderne Ansätze beschäftigen sich mit Erweiterungen bzw. Modifikationen der WBM, um sie flexibler für geometrisch komplexe Strukturen zu gestalten, sie für zeitabhängige Anregungen nutzbar zu machen und ihr Anwendungsfeld zu erweitern. In [Deckers et al 2014] wird ein Überblick über die verschiedenen Weiterentwicklungen der WBM gegeben, die überwiegend in der Noise and Vibration Research Group der KU Leuven erzielt wurden.
Anwendungen
Beschreibung eines 2D Halbraums
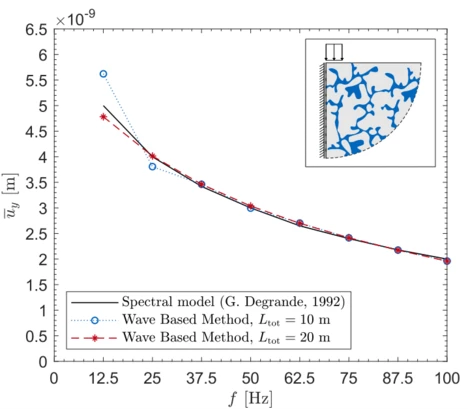
Mit der WBM wird ein Problem in mehrere Elemente unterteilt, deren Verschiebungs- und Spannungsfelder durch Wellenfunktionen angenähert werden. Eine große Herausforderung besteht darin, einen unendlich ausgedehnten Halbraum durch ein numerisches Modell abzubilden, welches auf einzelnen Elementen mit räumlichen Grenzen basiert. Verschiedene Konzepte absorbierender Randbedingungen wurden entwickelt, um die Sommerfeldsche Abstrahlbedingung näherungsweise zu erfüllen. Diese Bedingung besagt, dass die Energie in einem System ins Unendliche abstrahlt und nicht aus dem Unendlichen in das System gelangt. Um die Sommerfeldsche Abstrahlbedingung zu approximieren, wird für die WBM die absorbierende Randbedingung aus [Degrande and De Roeck 1993] gewählt, welche bzgl. einem Ortsvektor und für eine Frequenz definiert ist. Die Herleitung dieser Absorptionsrandbedingung basiert auf der analytischen Lösung für ein poröses Medium und ermöglicht eine perfekte Absorption senkrecht einfallender Wellenfronten. Abb. 5 zeigt beispielhaft ein zweidimensionales poroelastisches Bodenmodell mit einer Oberflächenlast. Die mittlere vertikale Verschiebungsamplitude wird unter dem belasteten Streifen für mehrerer Anregungsfrequenzen ausgewertet. Die Ergebnisse zeigen, dass das WBM-Modell mit einer Absorptionsrandbedingung die Referenzlösung hinreichend genau annähert.
Modellierung einer Wellenbarriere
Ein WBM-Modell kann zudem an andere Teilsysteme gekoppelt werden, um Wechselwirkungen zwischen Boden und Bausubstanz zu modellieren. Beispielsweise wurde ein Kopplungsansatz entwickelt, um eine Spundwand mit einem poroelastischen Halbraum zu verbinden. Die Spundwand wird durch ein Euler-Bernoulli- oder Timoschenko-Balkenmodell beschrieben. Abb. 6 zeigt die Normal- und Tangentialspannungen zwischen einem Balken und zwei gekoppelten WBM-Elementen. Diese Spannungen hängen von den Wellenfunktionen des linken bzw. rechten Bereichs ab und erzeugen Längs- und Vertikalverschiebungen entlang der Balkenachse. Um den Balken mit seinen angrenzenden WBM-Elementen zu verbinden, werden Element- und Kopplungsmatrizen berechnet, die zum globalen linearen Gleichungssystem beitragen. Zusätzlich müssen Randbedingungen für den Balken formuliert und dem Gleichungssystem hinzugefügt werden. In diesem Beispiel wird angenommen, dass die Spundwand freie Enden besitzt, sodass an diesen Punkten die Balkenschnittgrößen zu null angenommen werden können.
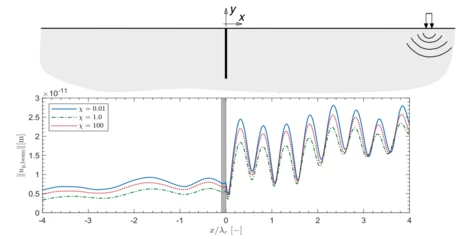
Spundwände können Bodenerschütterungen reduzieren, die durch Rayleigh-Wellen verursacht werden. Eine Zugdurchfahrt kann solche Oberflächenwellen erzeugen. Abb. 6 zeigt Verschiebungsamplituden, die entlang der Oberfläche eines Bodenmediums mit einer Spundwand berechnet wurden. Das System wird einer Oberflächenlast ausgesetzt und für verschiedene Kopplungsgrade zwischen Wasser- und Feststoffphase im Boden getestet. Die höchsten Verschiebungsamplituden ergeben sich bei einer starken Kopplung (blaue Kurve) sowie bei einer losen Kopplung (rote Linie). Bei einem mittleren Kopplungsgrad (grüne Linie) zwischen Flüssigkeits- und Feststoffphase führt dies zu einer Erhöhung der viskosen Dämpfung im System, sodass vergleichbar geringe Verschiebungsamplituden erzeugt werden.
Wellenstreuung an einer Oberflächenunregelmäßigkeit
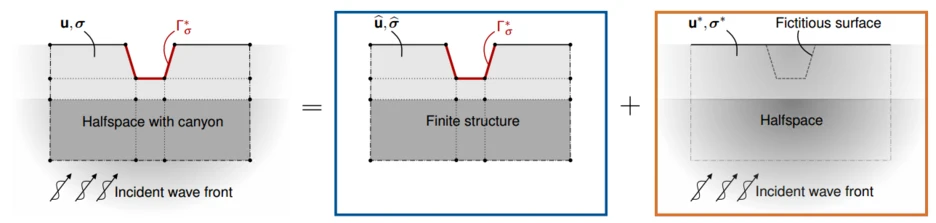
Bodenerschütterungen können auch durch schräg einfallende Wellenfronten verursacht werden, die häufig mit Reflexions-, Brechungs- und/oder Modenkonversionsprozessen kombiniert sind. Einfallende Wellenfronten können durch Erdbeben, unterirdische Züge oder Energieerzeugungsprozesse (z. B. Bohrplattformen, geothermische Kraftwerke) entstehen. Abb. 7 zeigt das Beispiel eines geschichteten Bodens mit einer Vertiefung, welche beispielsweise einem ausgetrockneten Flussbett entspricht. Das System wird in ein gestreutes Wellenfeld und eine Freifeldlösung unterteilt. Das gestreute Wellenfeld wird als Randwertproblem mit der WBM modelliert. Die Freifeldlösung bezieht sich auf eine einfallende Wellenfront, die entlang der Oberfläche des geschichteten Halbraums ohne Vertiefung reflektiert wird. Um die Freifeldlösung zu berechnen, wird die direkte Steifigkeitsformulierung nach [Degrande and De Roeck 1992] angewendet. Die Oberfläche der Vertiefung ist in Abb. 7 rot hervorgehoben und entspricht einer fiktiven Oberfläche in der Freifeldlösung. Die Lösungen für das gestreute Wellenfeld und das Freifeld werden entlang dieser Grenze gekoppelt, um die Bedingung einer unbelasteten Oberfläche zu erfüllen. Dazu werden zusätzliche Residuen bzw. Fehlerfunktionen formuliert und schwach erzwungen. Nach der Lösung des globalen linearen Gleichungssystems wird die Gesamtantwort des Systems durch Überlagerung der Lösung für das gestreute Wellenfeld mit der Freifeldlösung berechnet.
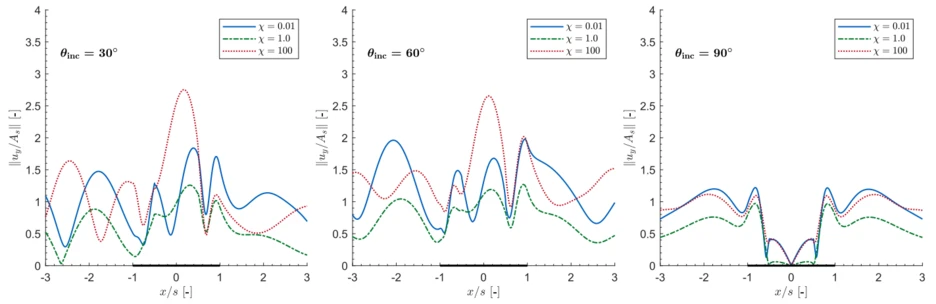
In Abb. 8 sind vertikale Verschiebungsamplituden dargestellt, die entlang der Oberfläche eines Bodenmediums und der Vertiefung ausgewertet werden. Diese werden für eine einfallende S-Welle berechnet. Es werden verschiedene Einfallswinkel und Kopplungsgrade zwischen der Flüssigkeits- und Feststoffphase getestet. Die höchsten Verschiebungsamplituden ergeben sich bei starker Kopplung (blaue Kurve) und loser Kopplung (rote Linie). Bei einem mittleren Kopplungsgrad (grüne Linie) zwischen Flüssigkeits- und Feststoffphase führt dies zu einer Erhöhung der viskosen Dämpfung im System, sodass vergleichbar geringe Verschiebungsamplituden erzeugt werden.
Die hier dargestellten numerischen Beispiele werden im Frequenzbereich berechnet und können durch Anwendung der inversen Fourier-Transformation in den Zeitbereich überführt werden. Dies ermöglicht die Vorhersage von Erschütterungen, die durch ein zeitabhängiges Signal (nicht-harmonische Anregung) verursacht werden, wie beispielsweise ein Erdbeben. Abb. 9 zeigt beispielsweise ein Video für das vertikale Verschiebungsfeld eines poroelastischen, geschichteten Bodens mit einer Vertiefung und einer schräg einfallenden S-Welle. Diese Wellenfront wird mit einer Ricker-Wavelet beschrieben. Die Wasserphase des Bodens und die Feststoffkörner sind durch eine lose Kopplung charakterisiert. Dadurch wird das Bodenmaterial kaum durch viskose Dämpfung beeinflusst. Dieser Zustand der losen Kopplung ermöglicht die Visualisierung einer zweiten P-Welle (P2-Welle), die charakteristisch für ein poroelastisches Medium ist, welches mit Hilfe der Biot-Theorie beschrieben wird. Das Video in Abb. 9 zeigt zunächst die Ankunft einer schräg einfallenden S-Welle, die innerhalb der oberen Bodenschicht in eine S- und eine P2-Welle gebrochen wird. Diese erzeugen ein gestreutes Wellenfeld um die Vertiefung und generieren Oberflächenwellen, die sich von der Vertiefung weg ausbreiten.
Weiterführende Literatur
- Lainer, Mirjam: A Wave Based Method for the analysis of a poroelastic system with a harmonic or time dependent excitation. Dissertation, 2025, doi: 10.13140/RG.2.2.33805.86247.
- Lainer, Mirjam; Müller, Gerhard: A wave based approach for the assessment of fluid–solid coupling for a scattered wave field at an empty canyon. Soil Dynamics and Earthquake Engineering 200, 2026, 109827, doi: 10.1016/j.soildyn.2025.109827.
- Lainer, Mirjam; Müller, Gerhard: Efficient treatment of a thin-walled wave barrier in a (poro)elastic structure with the Wave Based Method. Computers and Geotechnics 186, 2025, 107409, doi: 10.1016/j.compgeo.2025.107409.
Lainer, M.; Taddei, F.; Müller, G.: A Wave Based Method for the analysis of a fully and partially saturated halfspace under harmonic loading. Computers & Structures, 2023, doi: 10.1016/j.compstruc.2023.107040.