WBM analysis of saturated elastodynamic structures
Introduction
The Wave Based Method (WBM) belongs to the family of indirect Trefftz methods and uses weighted wave functions in order to model boundary value problems. These wave functions have to satisfy the underlying differential equations and usually violate the boundary conditions of a WBM element. A weighted residual formulation permits to minimize this error by determining the weighting factor for each wave function. By applying the WBM to a 2D saturated soil structure, the propagation of two longitudinal waves and one shear wave is modeled. In compliance with Biot’s theory, the field variables consist of displacement components in the solid phase and seepage components in the fluid, which influence the damping process within the structure. In order to fulfill the Sommerfeld radiation condition, this model is extended by an absorbing boundary condition, which transmits incident waves.
Description of an unsaturated elastodynamic medium
For a saturated elastodynamic structure the displacement field consists of solid phase displacements and a fluid seepage field. These are related to strains by the following compatibility condition, which contains a fourth strain value which is interpreted as the change of the fluid content.
\begin{equation}
\begin{pmatrix}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\gamma_{xy}\\
\zeta\\
\end{pmatrix} =
\begin{bmatrix}
\frac{\partial}{\partial x} & 0 & 0 & 0\\
0 & \frac{\partial}{\partial y} & 0 & 0\\
\frac{\partial}{\partial y} & \frac{\partial}{\partial x} & 0 & 0\\
0 & 0 & \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \\
\end{bmatrix}
\begin{pmatrix}
u_x\\
u_y\\
U_x\\
U_y\\
\end{pmatrix}
\end{equation}
Considering the first and second Lamé coefficients, the Young's E-Modulus and the two Biot coefficients, the plane strain constitutive relation is formulated as shown next. This relation contains an additional stress value which extends the classical Lamé theory and refers to a hydrostatic stress state.
\begin{equation}
\begin{pmatrix}
\sigma_{xx}\\
\sigma_{yy}\\
\tau_{xy}\\
\sigma_f\\
\end{pmatrix}=
\begin{bmatrix}
\lambda + 2\mu + \alpha^2 M & \lambda + \alpha^2 M & 0 & \alpha M\\
\lambda + \alpha^2 M & \lambda + 2\mu + \alpha^2 M & 0 & \alpha M\\
0 & 0 & \mu & 0\\
\alpha M & \alpha M & 0 & M\\
\end{bmatrix}
\begin{pmatrix}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\gamma_{xy}\\
\zeta\\
\end{pmatrix}
\end{equation}
By applying a Helmholtz approach, the deformation field in the solid phase and in the seepage field are decomposed into two irrotational potentials and one solenoidal potential:
\begin{align}
\mathbf{u}^s &= \boldsymbol{\nabla} \Phi_{p_1} + \boldsymbol{\nabla} \Phi_{p_2} + \boldsymbol{\widetilde{\nabla}} \Psi_s
\label{displ_field_old1}\\
\mathbf{U} &= \gamma_{p_1} \boldsymbol{\nabla} \Phi_{p_1} + \gamma_{p_2} \boldsymbol{\nabla} \Phi_{p_2} + \gamma_{s} \boldsymbol{\widetilde{\nabla}} \Psi_s
\label{displ_field_old2}
\end{align}
In order to evaluate the components of the seepage field, the two irrotational potentials and the solenoidal potential have to be scaled with three unknown values. These parameters are derived within a decoupling procedure of the underlying Navier equations. Such a decoupling procedure may be for example an eigenvalue problem.
Application of the Wave Based Method (WBM)
According to the Wave Based Method, the two irrotational potentials and the solenoidal potential are described by a finite number of wave functions, which fulfill the underlying differential equations and are derived within an analytical procedure. The displacement fields are approximated by a predefined number of weighted wave functions for the 1st and 2nd P-wave as well as for the S-wave.
\begin{align}
&\mathbf{u}^s_h \cong \mathbf{\widehat{u}}^s_h = \sum_{i = 1}^{n_{p_1}}c_{p_1,i} \boldsymbol{\nabla} \Phi_{p_1,i} + \sum_{j = 1}^{n_{p_2}}c_{p_2,j} \boldsymbol{\nabla} \Phi_{p_2,j} + \sum_{k = 1}^{n_{s}}c_{s} \boldsymbol{\widetilde{\nabla}} \Psi_{s,k} \\
&\mathbf{U}_h \cong \mathbf{\widehat{U}}_h = \sum_{i = 1}^{n_{p_1}}\gamma_{p_1} c_{p_1,i} \boldsymbol{\nabla} \Phi_{p_1,i} + \sum_{j = 1}^{n_{p_2}}\gamma_{p_2} c_{p_2,j} \boldsymbol{\nabla} \Phi_{p_2,j} + \sum_{k = 1}^{n_{s}}\gamma_{s} c_{s,k} \boldsymbol{\widetilde{\nabla}} \Psi_{s,k}
\end{align}
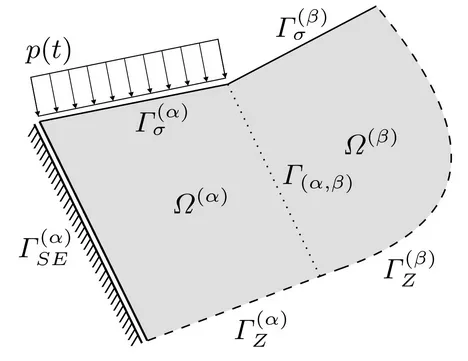
These weighting values are the unknowns within this approach and are supposed to be computed when applying the WBM approach. In order to derive the unknown weighting values, residuals along the boundaries of each domain are defined. These residuals are used for a weighted residual formulation. In this procedure the predefined wave functions are weakly enforced to fulfill the boundary conditions along the adjoining edges. Additionally, a Galerkin approach is used in order to apply the wave functions as weighting functions. These boundary conditions (BC) may be classified as follows and are illustrated in the attached figure.
- Dirichlet BC
- Neumann BC
- Coupling/continuity conditions
- Mixed BC (e.g. sliding edge)
- Absorbing BC (important for the Sommerfeld radiation condition)
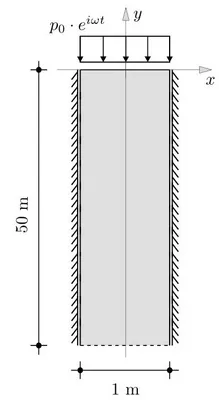
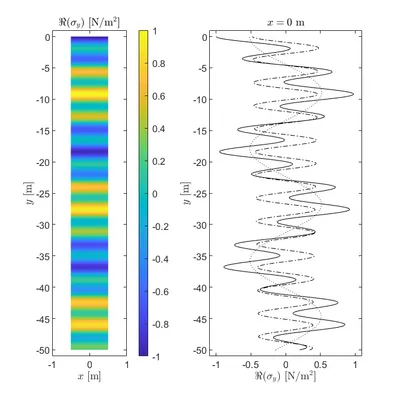
Numerical example: 1D soil column
The following figure shows a saturated soil column (Molsand soil) which is tested for an excitation frequency of 100Hz and a relatively high hydraulic conductivity of 1m/s. The latter value indicates the ability of the enclosed fluid to move within the pores and may be used to interpret the influence of the structure on the decay of the wave amplitudes. The attached plots include a surface plot which shows the distribution of the real part of the stresses in y-direction. This distribution contains contributions from the 1st and 2nd P-wave. In order to show the influences from both waves on the stress distribution, line plots have been evaluated for the soil column at x = 0m. It can been seen that the 1st P-wave has a larger wave length than the 2nd P-wave. Both waves hardly decline within the simulated lentgh of the soil column and both have a dominant effect on the total wave pattern.