Simulation in Applied Mechanics

Members

Mission Statement

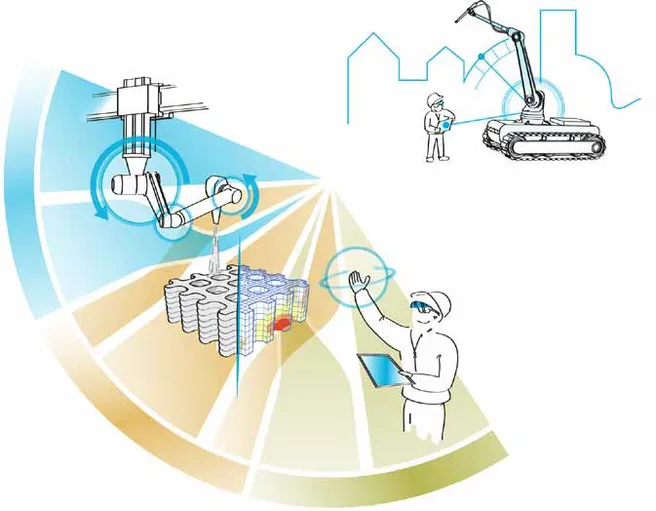
We develop new efficient highly accurate and well parallelizable methods for computational mechanics. Our developments are driven by both, pure scientific interest and industrial use cases.

The Finite Cell Method: connecting geometric models and simulation

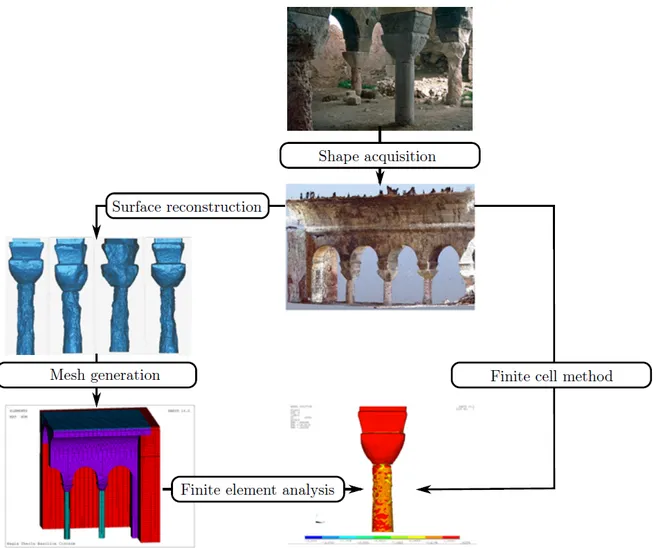
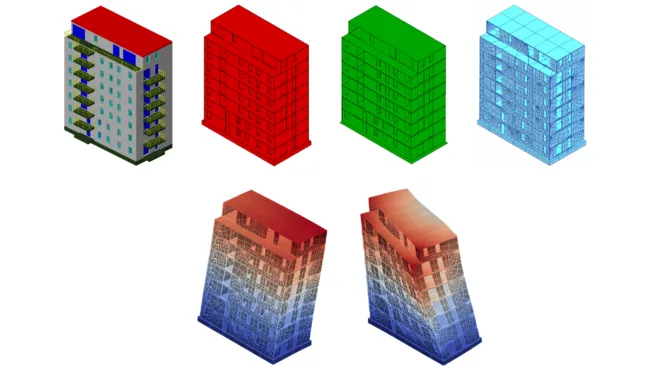
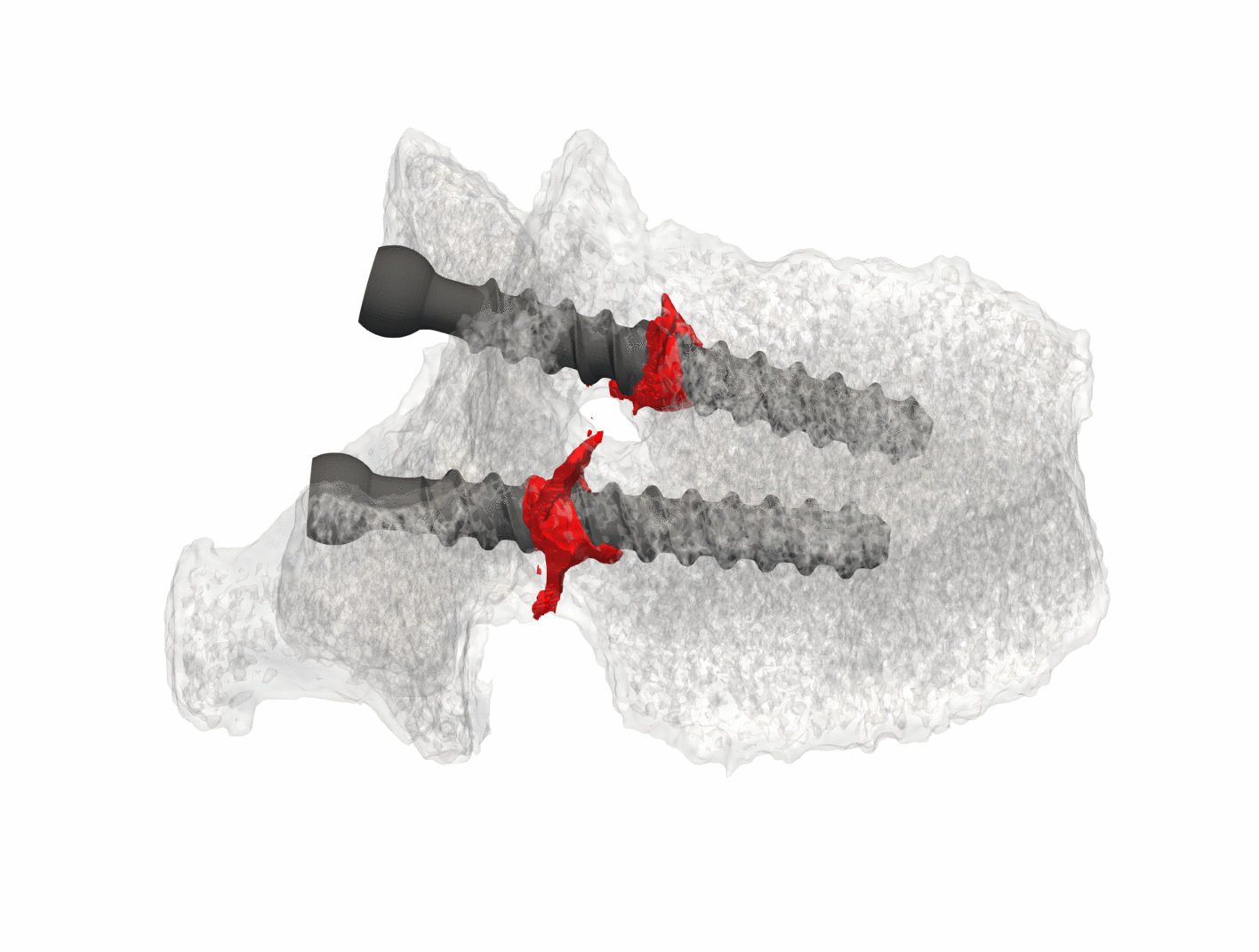
Every simulation starts from geometric models. We develop new methods for their seamless connection to analysis. To this end we have continuously developed the finite cell method (FCM) [1]. At its core, the FCM is an embedded domain method of high order. FCM allows to circumvent boundary conforming mesh generation. Thereby, it enables computations directly on CSG [2], V-Rep [3] or B-Rep models which may even be flawed [4]. It is also possible to directly simulate the mechanical behavior of artifacts on image data such as CT-Scans. Even direct computations on point clouds as obtained from laser scans or as generated from pictures are now possible [5].

It is interesting to note that, even though non-boundary conforming meshes are employed, the finite cell method is able to preserve the convergence rate of the underlying Galerkin-type discretization scheme.

hp-discretization schemes

We develop new discretization techniques for high order finite element discretizations of various types. Specifically, we advance refinement technologies in Isogeometric Analysis [6,7] and create new adaptive hp-type refinements in classical finite elements of high order be it in form of the multi-level hp-method [8] or using constraint matrices [9].

Overlay mesh construction for the multi-level hp-method [8]

Numerical approximation of the gradient of a shock wave [8]

We continue to push the boundaries by developing hp-type discretizations for arbitrary dimensions which will be used in space-time finite elements to simulate transient processes. These include heat and phase changes which occur in modern production processes such as additive manufacturing or wave propagation phenomena useful in non-destructive testing.

Projects (selection)

Additive Manufacturing - process simulation

Constructive Solid Geometriy, B-Rep and V-Rep Analysis

Additive Manufacturing in Construction - The Challenge of Large Scale -

Efficient Parallel Computation for the Finite Cell Method

Structural Properties of Additively Manufactured Metal Parts by Homogenization

Numerical Analysis of Human Vertebrae

Image-based Finite Element Analysis

BIM-Coupled Vibroacoustic Simulation

Fracture Mechanics

Non-Destructive Testing using Full Wave Form Inversion

Organizational Structures in Massively Distributed Systems for Numerical Computations

References

Düster, Alexander, Ernst Rank, and Barna Aladar Szabó. “The P-Version of the Finite Element Method and Finite Cell Methods.” In Encyclopedia of Computational Mechanics, edited by E. Stein, R. Borst, and T. J. R. Hughes, 2:1–35. Chichester, West Sussex: John Wiley & Sons, 2017.
Wassermann, Benjamin, Stefan Kollmannsberger, Tino Bog, and Ernst Rank. “From Geometric Design to Numerical Analysis: A Direct Approach Using the Finite Cell Method on Constructive Solid Geometry.” Computers & Mathematics with Applications, January 3, 2017. https://doi.org/10.1016/j.camwa.2017.01.027
Wassermann, Benjamin, Nina Korshunova, Stefan Kollmannsberger, Ernst Rank, and Gershon Elber. “Direct Simulation of Functionally Graded Materials Using V-Models and the Finite Cell Method,” 2020, status submitted
Wassermann, Benjamin, Stefan Kollmannsberger, Shuohui Yin, László Kudela, and Ernst Rank. “Integrating CAD and Numerical Analysis: ‘Dirty Geometry’ Handling Using the Finite Cell Method.” Computer Methods in Applied Mechanics and Engineering 351 (July 1, 2019): 808–35. https://doi.org/10.1016/j.cma.2019.04.01
Kudela, László, Stefan Kollmannsberger, Umut Almac, and Ernst Rank. “Direct Structural Analysis of Domains Defined by Point Clouds.” Computer Methods in Applied Mechanics and Engineering 358 (January 1, 2020): 112581. https://doi.org/10.1016/j.cma.2019.112581.
D’Angella, Davide, Stefan Kollmannsberger, Ernst Rank, and Alessandro Reali. “Multi-Level Bézier Extraction for Hierarchical Local Refinement of Isogeometric Analysis.” Computer Methods in Applied Mechanics and Engineering 328 (January 2018): 147–74. https://doi.org/10.1016/j.cma.2017.08.017.
Kollmannsberger, Stefan, Davide D’Angella, Ernst Rank, Wadhah Garhuom, Simeon Hubrich, Alexander Düster, Paolo Di Stolfo, and Andreas Schröder. “Spline‐ and Hp‐basis Functions of Higher Differentiability in the Finite Cell Method.” GAMM-Mitteilungen 43, no. 1 (March 2020). https://doi.org/10.1002/gamm.202000004.
Zander, Nils, Tino Bog, Mohamed Elhaddad, Felix Frischmann, Stefan Kollmannsberger, and Ernst Rank. “The Multi-Level hp-Method for Three-Dimensional Problems: Dynamically Changing High-Order Mesh Refinement with Arbitrary Hanging Nodes.” Computer Methods in Applied Mechanics and Engineering 310 (October 1, 2016): 252–77. https://doi.org/10.1016/j.cma.2016.07.007.
Di Stolfo, Paolo, Andreas Schröder, Nils Zander, and Stefan Kollmannsberger. “An Easy Treatment of Hanging Nodes in Hp-Finite Elements.” Finite Elements in Analysis and Design 121 (November 15, 2016): 101–17. https://doi.org/10.1016/j.finel.2016.07.001.

Former Members

Benjamin Wassermann
Dr.-Ing.
now @ SOFiSTiK

Jing Rao
Prof. Dr.-Ing.
now @ UNSW

Alexander Paolini

now @ SOFiSTiK

John Jomo
Dr.-Ing.
now @ LS-DYNA

Nina Korshunova
Dr.-Ing.
now @ DirectFEM

Lászó Kudela
Dr.-Ing.
now @ DirectFEM

Davide D'Angella
Dr.-Ing.
now @ DirectFEM

Christoph Ertl

now @ TEBIS