Constructive Solid Geometry, B-Rep and V-Rep Analysis
Team Members: Benjamin Wassermann, Stefan Kollmannsberger, Ernst Rank
Funding: German Research Fundation (DFG 624/22)
Duration: 05.2014-11.2019
Project description
The numerical analyses of models require suitable representations, most commonly meshes. The transition process from a CAD model to a simulation model for a classical finite element analysis (i.e. a mesh) can consume up to 80% of the engineering effort. Typically, this transition process involves the following steps:
- First the model needs to be prepared to be meshable. I.e. all modeling flaws, such as gaps, intersections, multiple entities, etc. need to be healed. This step is only partially automatable, as some flaws allow for various ways of interpretation of originally desired exact topology and shape.
- The model is meshed. This process is fully automatable. However, it imposes strong requirements to the underlying model (see step 1).
- The resulting mesh typically needs to be adjusted such that the mesh quality is sufficient for the subsequent FEM analysis.
To circumevent this costly conversion process, several methods were developed, which perform a simulation directly on the original geometry. The most prominent example is Isogoemetric Analysis (IGA), which uses the same shape functions for the geometric representation and the simulation. Consequently, meshing and mesh healing can be omitted.
However, IGA still requires the geometry to be valid in the sense that it is analysis suitable. For three dimensions this means that a volume is discribed by means of boundary conforming, non overlapping topological hexahedrals. These rather strict reqironments may be lifted by the Finite Cell Method.
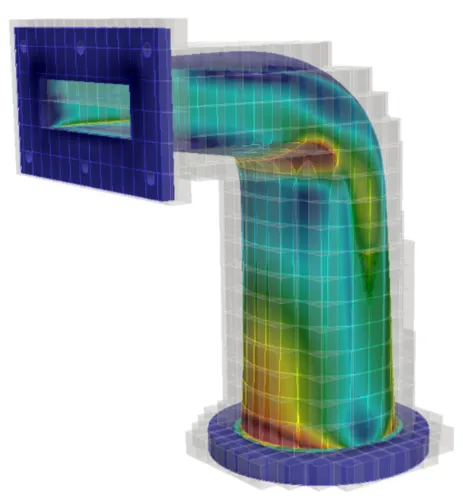
Finite Cell Method
The Finite Cell Method (FCM) is a high-order ficitious domain method. The complex geometry is embedded into a simple domain that can be meshed easily in a regular grid.

The numerical integration of the weak formulation is extended to the whole domain. Integration points are then weighted, respectively to their location inside or outside of the pyhiscal domain. Hence, the complexity of the geometry is resolved on the integration level, which poses far less strict requirements on the model. It is in fact sufficient to provide a reliable point membership classification. To this end, various models may be integrated among them: Constructive Solid Geometries, Boundary representation models which may even be flawed, or more involved volume representations.
Constructive Solid Geometries
Constructive Solid Geometries (CSG) CAD models are constructed from a set of primitives such as spheres, cuboids, cylinders, etc., which are combined with the Boolean operations: union, intersection and difference.
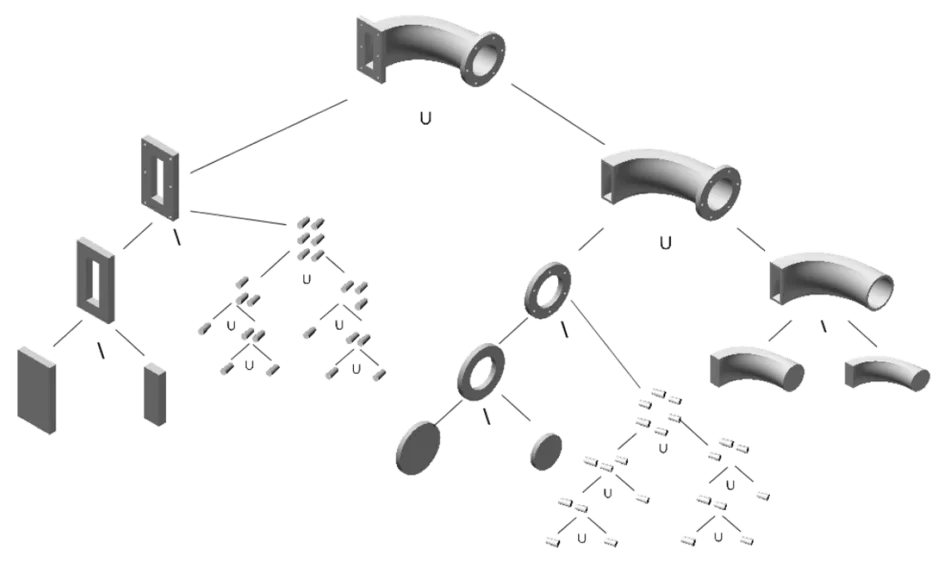
The point membership classification for the FCM can be carried out easily on a CSG tree of simple primitives and was extended to obtain point membership information also from more elaborate primitives, such as sweeps, lofts, etc.
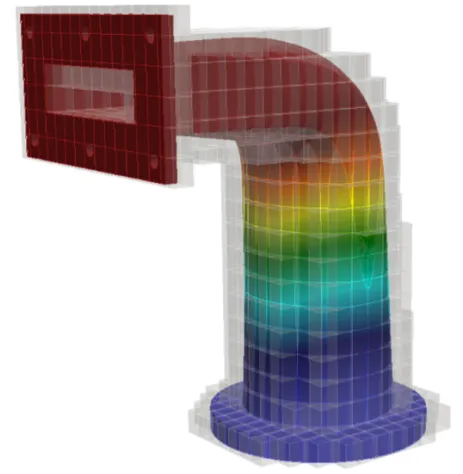
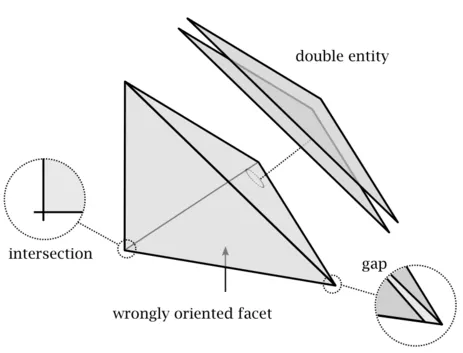
Flawed Boundary Representation Models
B-Rep models are prone to geometrical and topological errors, such as gaps, intersections, missing or double entities, etc. These flaws can destroy a numerical simulation and thus would typically require geometry healing. However, a method, based on Octree reconstruction and the Floodfill algorithm was developed which allows a direct use of flawed geometries in computer aided engineering. To this end, the model is resolved by an octree, whose smallest leaf cells are larger than the characteristric size of the largest gap. Hence, a subsequently applies floodfill algorithm can mark all octree cells as inside and outside.
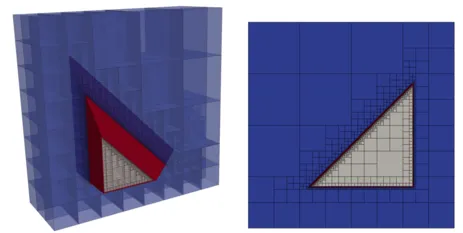
To improve the accuracy, serveral additional ray-casting test are carried out for the integration points on the leaf cells. The domain membership is then evaluated by a 'vote for the majority'.
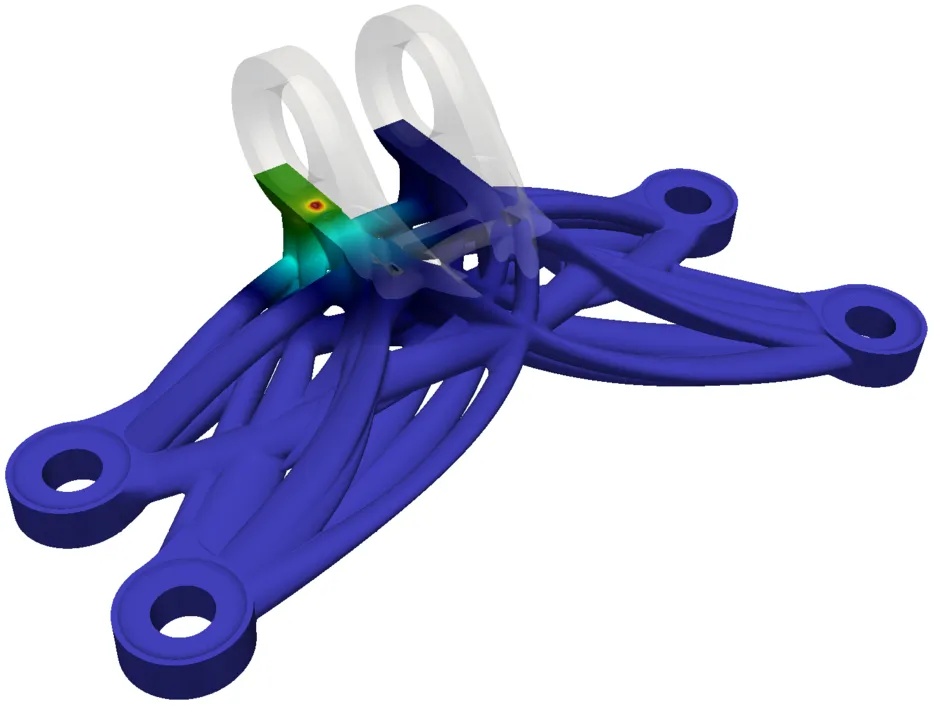
Volumetric Representation
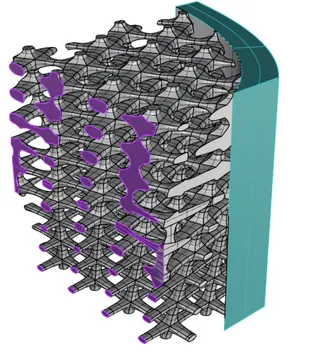
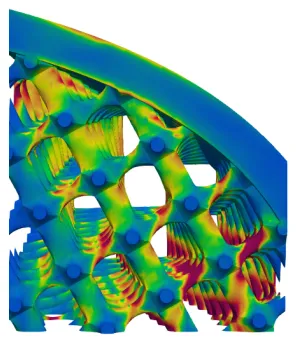
With the V-Rep framework developed by Elber et al. at the Technion University, a CAD representation is available which allows to explicitly model the interior volume. V-Reps consist of non-singular trimmed trivariate B-Splines, or NURBS. These can be used by the FCM to simulate functionally graded materials. To this end, the parameters of the control points are extended such that they carry additional parameters, such as Young's modulus, or thermal conductivity.
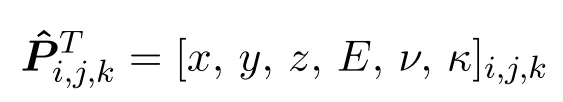
The values for the material parameters need, of course, to be provided beforehand and are then fitted to the spline description, e.g. using the method of Least Squares.


Besides multi-material functionally graded materials, the V-Rep framework allows also for modeling materials, which change their properties through a continuously varying microstructure.