Material characterization of Additively Manufactured Metal Porous Parts
| Project team leader | Dr.-Ing. habil. Stefan Kollmannsberger (TUM), Prof. Dr. rer.nat. Ernst Rank (TUM) |
| PhD student | Nina Korshunova, M.Sc. (hons.) (TUM) |
| Project partners | Dr. Daniel Reznik (Siemens AG), Prof. Dr.-Ing. habil. Alexander Düster (TUHH) |
| Sponsorship | Research and Technology Center, Siemens AG, Corporate Technology ; International Graduate School of Science and Engineering - IGSSE |
Project description
Motivation
Recent developments in additive manufacturing have provided a unique possibility to create complex structures with porosity on micro and meso-structural levels. Such designs can outperform conventional materials in specific industrial applications, e.g. turbine blades with a transpiration cooling. However, the high flexibility of the input parameters for the 3D printers, such as the laser diameter, hatch distance etc., challenges a reliable estimation of the mechanical behaviour of the final parts. Moreover, a high variation of porosity in all material directions limits the application of analytical bounds based on the void fraction ratio.
Why numerical homogenization?
Numerical homogenization is an efficient and robust alternative to perform non-destructive evaluation of the material characteristics based on high resolution finished: 3D images of produced specimens. The Heterogeneous Multiscale Methods (HMM), which is the scope of current work, differ by the data-driven coupling strategies. The most intuitive sequential homogenization approach does not provide a reliable estimate for nonlinear or dynamic computations, as the micro-structure does not include the current state of the macroscopic deformation (see e.g. [1]). Developments in concurrent multi-scale homogenization methods made them more attractive as they allow to keep an information about a current state of deformation for a macroscopic point (see e.g. [2]). The micro-scale is incorporated in an iterative procedure of concurrent "localization-homogenization" steps (see Figure 1). When for the solution of both scales Finite Element Method is used, the method is called FE2 homogenization approach. This method is employed in the current work.
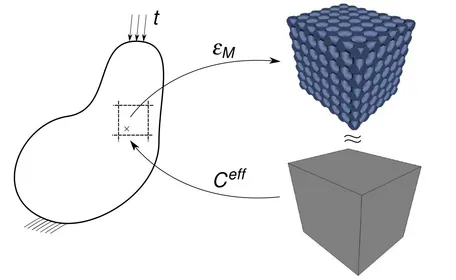
Numerical approach
The conventional Finite Element Method applied to numerical homogenization leads to a labor intensive meshing procedure to extract the representative volume elements that makes it impractial from the industrial point of view. Furthermore, non-symmetric micro-architectured structures make it difficult to apply correct boundary conditions for the solution of the microstructural boundary value problem.
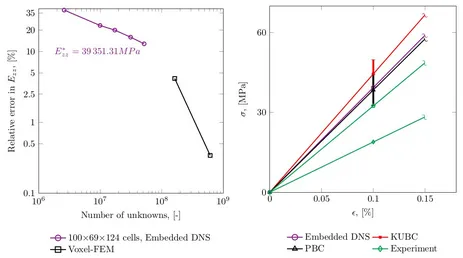
To address these issues, in the scope of the current project the Finite Cell Method [3] is employed. Application of the homogenization boundary conditions in case of the voids crossing the boundary remains difficult. The extensive research studies on different boundary conditions are performed. Kinematic Uniform (KUBC), Static Uniform (SUBC) and Periodic Boundary conditions (PBC) are investigated in combination with the recently developed window method [4], [5]. The results are compared with the homogenized properties without the window and the efficiency of the different approaches is addressed.
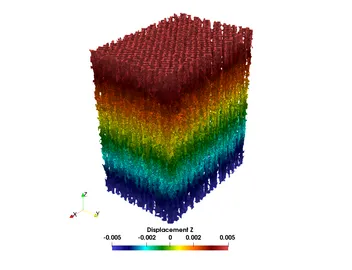
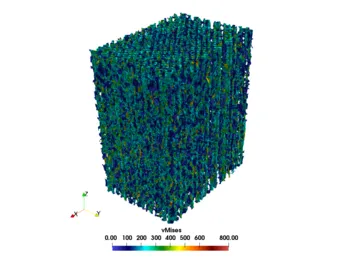
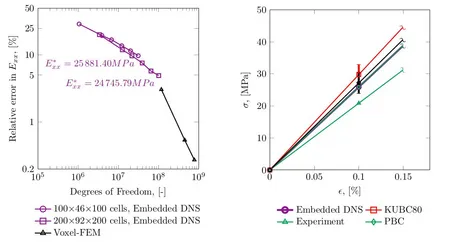
Currently, the road map is established and validated for the automatized numerical computation of the homogenized elasticity tensor of additively manufactured steel structures using 3D images (see Fig. 2 and Fig.3). Homogenization procedure run through the whole CT-Scan and statistical data on the homogenized properties is summarized. The computational results are verified with respect to a fully-resovled voxel-FEM computation of a complete specimen (see Fig.5). Validation of the proposed model is performed comparing the numerical results with the results stemming from experimental tests (see Fig.6 and Fig.7). Current stage of a project is focusing on a validation of non-linear elastic regime and a second-order homogenization.




References
- Nemat-Nasser, S. and Hori, M. (1999).
Micromechanics: Overall Properties of Heterogeneous Materials. North-Holland Series in Applie. Elsevier. - Kouznetsova, V., Geers, M., and Brekelmans, W. (2004).
Multi-scale second-order computational homogenization of multi-phase materials: a nested finite element solution strategy. Computer Methods in Applied Mechanics and Engineering, 193(48):5525 – 5550. Advances in Computational Plasticity. - Düster, A., Sehlhorst, H.-G., Rank, E. (2012)
Numerical homogenization of heterogeneous and cellular materials utilizing the finite cell method. Computational Mechanics, 50(4):413-431. - Hain, M., Wriggers, P. (2008)
Numerical homogenization of hardened cement paste. Computational Mechanics, 42(2): 197-212. - Heinze, S., Joulaian, M., and Düster, A. (2015)
Numerical homogenization of hybrid metal foams using the finite cell method. Computers Mathematics with Applications, 70(7):1501 – 1517.
Publications and conferences
-
Korshunova, N.; Jomo, J.; Lékó, G.; Reznik, D.; Balázs, P.; Kollmannsberger, S.
Image-based material characterization of complex microarchitectured additively manufactured structures
Computers and Mathematics with Applications, 2019 - Status: Preprint / submitted
-
Korshunova N., Jomo J., Reznik D., Kollmannsberger S., Rank E.
From CT-Scans to material characterization: mechanical behavior of micro-porous metal structures
In: High-Order Finite Element and Isogeometric Methods, 2019
-
Korshunova, N., Jomo, J., Reznik, D., Kollmannsberger, S., Rank, E.
Material characterization of additively manufactured complex steel components
In: Simulation for Additive Manufacturing (Sim-AM 2019), 2019
-
Jomo J., Korshunova N., Carraturo M., Kollmannsberger S., Mundani R. P., Rank E.
A parallel immersed finite element framework for numerical computations of metal additive manufacturing processes and products
In: II International Conference on Simulation for Additive Manufacturing, Pavia, Italy, 2019
-
Korshunova, N., Jomo, J., Reznik, D., Kollmannsberger, S., Düster, A., Rank, E.
From images to material characterization of additively manufactured micro-architectured structures
In: 13th World Congress in Computational Mechanics, 2018
-
Korshunova, N.; Reznik, D.; Kollmannsberger, R.; Rank, E.
Numerical simulation of material parameters of additively manufactured porous metal parts
In: 1st ECCOMAS Thematic Conference on Simulation for Additive Manufacturing, 2017
Contact: Nina Korshunova, M.Sc. (hons.)